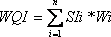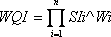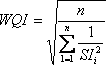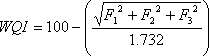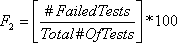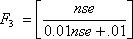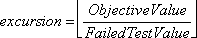Why the Water Quality Definition Requires Multiple Models

In the Part 2 of this three-part series, we quickly review the Water Quality Index (WQI) Development Process that concluded Part 1—the segment that proposed solving the water quality definition. Following this refresher to WQI development, we continue author Harbans Lal’s research into WQI modelling methodology that he has cited through extensive research on this subject. Setting aside subjective solutions to water quality definitions, please have one sharp pencil (with eraser), your capable calculator, and measurable water quality components ready to input as data into the following algorithmic models. (Remember these models as they will be utilized in actual situations in Part 3—the conclusion to this series.)

Introduction to the Water Quality Index (Part 2) By Harbans Lal

Expressing water quality information in a format that is simple and easily understood by common people

Reviewing the WQI Development Process

The process of developing a WQI involves the following steps:

1. Identify water quality parameters of interest and their ranges of acceptability for the intended uses of the water body.
2. Compare the measured value with the subjective rating curve and arriving at a dimensionless sub-index value (0–1) for each parameter.
3. Define the weighing factor and/or heuristics for each parameter to be considered while building an overall WQI.
4. Select an algorithm and computing the WQI with the available data and assumptions.

A number of algorithms (models) for calculating WQI have been developed and reported in the literature. Some of these include:

a) Weighted arithmetic mean (Cude 2001)- In this model, different water quality components are multiplied by a weighting factor and are then aggregated using simple arithmetic mean (Equation 1).

Equation 1:

Where WQI = Water Quality Index
SIi = Sub-index i
n = number of sub-indices
Wi = Weight given to sub-index i

Introduction to the Water Quality Index (Part 2) By Harbans Lal

1. Identify water quality parameters of interest and their ranges of acceptability for the intended uses of the water body.
2. Compare the measured value with the subjective rating curve and arriving at a dimensionless sub-index value (0–1) for each parameter.
3. Define the weighing factor and/or heuristics for each parameter to be considered while building an overall WQI.
4. Select an algorithm and computing the WQI with the available data and assumptions.

1. Ability to capture large variety of non-linear relations
2. Easily adoptable to local conditions
3. Could be interpreted verbally
4. Could include information that other methods cannot include such as individual knowledge and experience
5. Possibility of enhancing the results by combining qualitative information with the quantitative data that expresses the ecological status of the water body
6. Better handling of situations with missing data without affecting the results significantly

1. Scope—number of variables not meeting water quality objectives (Equation 4a),
2. Frequency—the number of times these objectives are not met (Equation 4b), and
3. Amplitude—amount by which the objectives are not met (Equation 4c).

c) Un-weighted harmonic square mean (Dojlido et al. 1994 cited by Cude 2001)- This model is considered an improvement over the weighted arithmetic mean and the weighted geometric mean. This allows the most impaired variable to impart the greatest influence on the water quality index and acknowledges that different water quality variables will pose differing significance to overall water quality at different times and locations (Equation 3).

Equation 3:

Where WQI = Water Quality Index
SIi = Sub-index i
n = number of sub-indices
Wi = Weight given to sub-index i

d) Using the fuzzy logic model (Lermontov et al. 2009 and Nasiri et al. 2007)- This model employs artificial intelligence (AI) concept and helps capture uncertainties and inaccuracies in knowledge data. It can represent qualitative knowledge and human inference process—quite common in expressing water quality parameters—without a precise quantitative analysis. This approach, as demonstrated by Lermontov et al. 2009 and Nasiri et al. 2007, presents the following advantages over the conventional numerical process:

1. Ability to capture large variety of non-linear relations
2. Easily adoptable to local conditions
3. Could be interpreted verbally
4. Could include information that other methods cannot include such as individual knowledge and experience
5. Possibility of enhancing the results by combining qualitative information with the quantitative data that expresses the ecological status of the water body
6. Better handling of situations with missing data without affecting the results significantly

e) Baseline comparative model (UNEP 2007)- This model compares water quality observations to benchmark values of different parameters instead of normalizing observed values to subjective rating curves. The benchmark values may be derived from national, state, or local water quality standards, or site-specific background values. The Canadian Council of Ministers of the Environment (CCME) used this approach for their model known as Canadian Water Quality Index (CWQI). The Global Environmental Monitoring System (GEMS)/Water Program of the United Nations Environment Program (UNEP) adopted and used the CWQI model for evaluating the quality of drinking water around the globe (UNEP 2007).

The CWQI (Equation 4) incorporates three elements:

1. Scope—number of variables not meeting water quality objectives (Equation 4a),
2. Frequency—the number of times these objectives are not met (Equation 4b), and
3. Amplitude—amount by which the objectives are not met (Equation 4c).

Equation 4:

Where WQI = Water Quality Index
F1 represents Scope: the percentage of parameters that exceeds the guideline (Equation 4a).
F2 represents Frequency: the percentage of individual tests within each parameters that exceeds the guideline (Equation 4b).
F3 represents Amplitude: the extent (excursion) to which the failed test exceed the guideline which includes a three-step process for calculation (Equation 4c).

Equation 4a:

Equation 4b:

Equation 4c:

Where nse (Normalized sum of excursion) is expressed as:

and

Where failed test value is greater than the objective value, for cases where test value must not fall below objective value, then

Similar to other WQIs, this model also produces a number between zero (worst water quality) and 100 (best water quality). In this case, the index is flexible in terms of the benchmarks that are used for calculations, and depends on the information required from the index. For example, guidelines for the protection of aquatic life may be used (when available) if the index is being calculated to quantify ecological health of the water, or drinking water quality guidelines may be used if the interest in the index is in drinking water safety.

The CCME WQI has been widely used in Canada. It has also been adopted by the UNEP for evaluating the quality of water in different countries around the globe. This model expresses well when a history of monitored data for different water quality parameters is available. It is recommend that at a minimum four variables sampled at least four times be used in calculation of the index for this approach (CCME 2001).

Please read the upcoming conclusion to this three-part series as our author applies and solves Water Quality Index models given the algorithms above in applicable solutions to the water-quality definition.